[이것이 코딩테스트다] 그래프 탐색 알고리즘 : DFS & BFS - 예제
2024.08.05 - [코딩테스트/AL] - [이것이 코딩테스트다] 그래프 탐색 알고리즘 : DFS & BFS
[이것이 코딩테스트다] 그래프 탐색 알고리즘 : DFS & BFS
대표적인 그래프 탐색 알고리즘에는 DFS와 BFS가 있습니다. 여기서 탐색이란 많은 양의 데이터 중에서 원하는 데이터를 찾는 과정을 말하며, DFS와 BFS는 코딩 테스트에서 매우 자주 등장하는 유
yeonnys.tistory.com
저번 글에 이어 이번에는 DFS와 BFS 알고리즘을 활용한 예제 문제를 설명해보겠습니다!
문제) 음료수 얼려 먹기
문제
Q. N × M 크기의 얼음 틀이 있습니다. 구멍이 뚫려 있는 부분은 0, 칸막이가 존재하는 부분은 1로 표시됩니다. 구멍이 뚫려 있는 부분끼리 상, 하, 좌, 우로 붙어 있는 경우 서로 연결되어 있는 것으로 간주합니다. 이때 얼음 틀의 모양이 주어졌을 때 생성되는 총 아이스크림의 개수를 구하는 프로그램을 작성하세요. 다음의 4 × 5 얼음 틀 예시에서는 아이스크림이 총 3개 생성됩니다.

문제에 따르면, 구멍이 뚫려 있는 부분끼리 상, 하, 좌, 우로 붙어 있는 경우 한 덩어리로 취급하므로,
아이스크림은 총 3개를 만들 수 있습니다.

이 문제는 연결 요소 찾기 문제로 볼 수 있습니다.
어떻게 해결할 수 있을까요?

풀이
이 문제는 DFS 혹은 BFS로 해결할 수 있습니다.
일단 앞에서 배운 대로 얼음을 얼릴 수 있는 공간이 상, 하, 좌, 우로 연결되어 있다고 표현할 수 있으므로
그래프 형태로 모델링 할 수 있습니다. 다음과 같이 3 × 3 크기의 얼음 틀이 있다고 가정하고 생각해 봅시다.

DFS를 활용하여 이 문제를 푸는 방법은 다음과 같습니다.
1. 특정한 지점의 주변 상, 하, 좌, 우를 살펴본 뒤에 주변 지점 중에서 값이 '0' 이면서 아직 방문하지 않은 지점이 있다면 해당 지점을 방문한다.
2. 방문한 지점에서 다시 상, 하, 좌, 우를 살펴보면서 방문을 진행하는 과정을 반복하면, 연결된 모든 지점을 방문할 수 있다.
3. 모든 노드에 대하여 1~2번 과정을 반복하며, 방문하지 않은 지점의 수를 카운트한다.
1. 입력 받기
먼저, 주어진 문제의 입력을 입력받습니다.
# N, M을 공백을 기준으로 구분하여 입력 받기
n, m = map(int, input().split())
# 2차원 리스트의 맵 정보 입력 받기
graph = []
for i in range(n):
graph.append(list(map(int, input())))
여기서 n과 m은 각각 얼음 틀의 세로 길이와 가로 길이를 나타냅니다.
2. DFS 함수 정의
# DFS로 특정한 노드를 방문한 뒤에 연결된 모든 노드들도 방문
def dfs(x, y):
# 주어진 범위를 벗어나는 경우에는 즉시 종료
if x <= -1 or x >= n or y <= -1 or y >= m:
return False
# 현재 노드를 아직 방문하지 않았다면
if graph[x][y] == 0:
# 해당 노드 방문 처리
graph[x][y] = 1
# 상, 하, 좌, 우의 위치들도 모두 재귀적으로 호출
dfs(x - 1, y)
dfs(x, y - 1)
dfs(x + 1, y)
dfs(x, y + 1)
return True
return False
위의 함수는 특정 노드를 방문하고, 그 노드와 연결된 모든 노드를 재귀적으로 방문하는 형태입니다.
주어진 노드가 0일 경우, 방문한 노드로 표시 (1) 하고 상, 하, 좌, 우로 이동하여 모든 연결된 얼음을 방문합니다.
3. 모든 위치를 탐색하며 DFS 수행
# 모든 노드(위치)에 대하여 음료수 채우기
result = 0
for i in range(n):
for j in range(m):
# 현재 위치에서 DFS 수행
if dfs(i, j) == True:
result += 1
이제 전체 얼음 틀을 순회하면서 각 위치에서 DFS를 수행합니다.
DFS가 성공적으로 수행되면, 새로운 아이스크림 덩어리를 찾은 것이므로,
result를 1 증가시킵니다.
전체 코드 및 동작 과정
전체적인 코드는 아래와 같습니다.
# N, M을 공백을 기준으로 구분하여 입력 받기
n, m = map(int, input().split())
# 2차원 리스트의 맵 정보 입력 받기
graph = []
for i in range(n):
graph.append(list(map(int, input())))
# DFS로 특정한 노드를 방문한 뒤에 연결된 모든 노드들도 방문
def dfs(x, y):
# 주어진 범위를 벗어나는 경우에는 즉시 종료
if x <= -1 or x >= n or y <= -1 or y >= m:
return False
# 현재 노드를 아직 방문하지 않았다면
if graph[x][y] == 0:
# 해당 노드 방문 처리
graph[x][y] = 1
# 상, 하, 좌, 우의 위치들도 모두 재귀적으로 호출
dfs(x - 1, y) # 상
dfs(x + 1, y) # 하
dfs(x, y - 1) # 좌
dfs(x, y + 1) # 우
return True
return False
# 모든 노드(위치)에 대하여 음료수 채우기
result = 0
for i in range(n):
for j in range(m):
# 현재 위치에서 DFS 수행
if dfs(i, j) == True:
result += 1
print(result) # 정답 출력
이제 예시를 들어, 동작 과정을 살펴봅시다!
4 5
00110
00011
11111
00000
위와 같은 입력이 주어질 때,
graph는 아래와 같이 구성되게 됩니다.
[
[0, 0, 1, 1, 0],
[0, 0, 0, 1, 1],
[1, 1, 1, 1, 1],
[0, 0, 0, 0, 0]
]
이 후, (0, 0) 위치에서 DFS를 시작하여 연결된 0들을 방문 처리 합니다.
-> graph[0][0] == 0 이기 때문에 해당 노드를 1로 바꾸고,
해당 위치의 상하좌우를 재귀함수로 호출합니다.
즉,
dfs(x - 1, y) # 상
-> (-1, 0) -> 범위 벗어남
dfs(x + 1, y) # 하
-> (1, 0)
dfs(x, y - 1) # 좌
-> (0, -1) -> 범위 벗어남
dfs(x, y + 1) # 우
-> (0, 1)
을 차례대로 호출하게 됩니다.

참고로 알고리즘 문제에서 위치는 위와 같이 표현합니다.
이 후, 위치를 차례대로 이동하며, 재귀함수를 수행하는 것입니다!
문제) 미로 탈출
문제
Q. 동빈이는 N × M 크기의 직사각형 형태의 미로에 갇혔습니다. 미로에는 여러 마리의 괴물이 있어 이를 피해 탈출해야 합니다.
동빈이의 위치는 (1, 1)이며 미로의 출구는 (N, M)의 위치에 존재하며 한 번에 한 칸씩 이동할 수 있습니다. 이때 괴물이 있는 부분은 0으로, 괴물이 없는 부분은 1로 표시되어 있습니다. 미로는 반드시 탈출할 수 있는 형태로 제시됩니다.
이때 동빈이가 탈출하기 위해 움직여야 하는 최소 칸의 개수를 구하세요. 칸을 셀 때는 시작 칸과 마지막 칸을 모두 포함해서 계산합니다.

풀이
BFS는 시작 지점에서 가까운 노드부터 차례대로 그래프의 모든 노드를 탐색합니다.
상, 하, 좌, 우로 연결된 모든 노드로의 거리가 1로 동일합니다.
따라서 (1, 1) 지점부터 BFS를 수행하여 모든 노드의 최단 거리 값을 기록하면 해결할 수 있습니다.
예시로 다음과 같이 3 x 3 크기의 미로가 있다고 가정해봅시다.


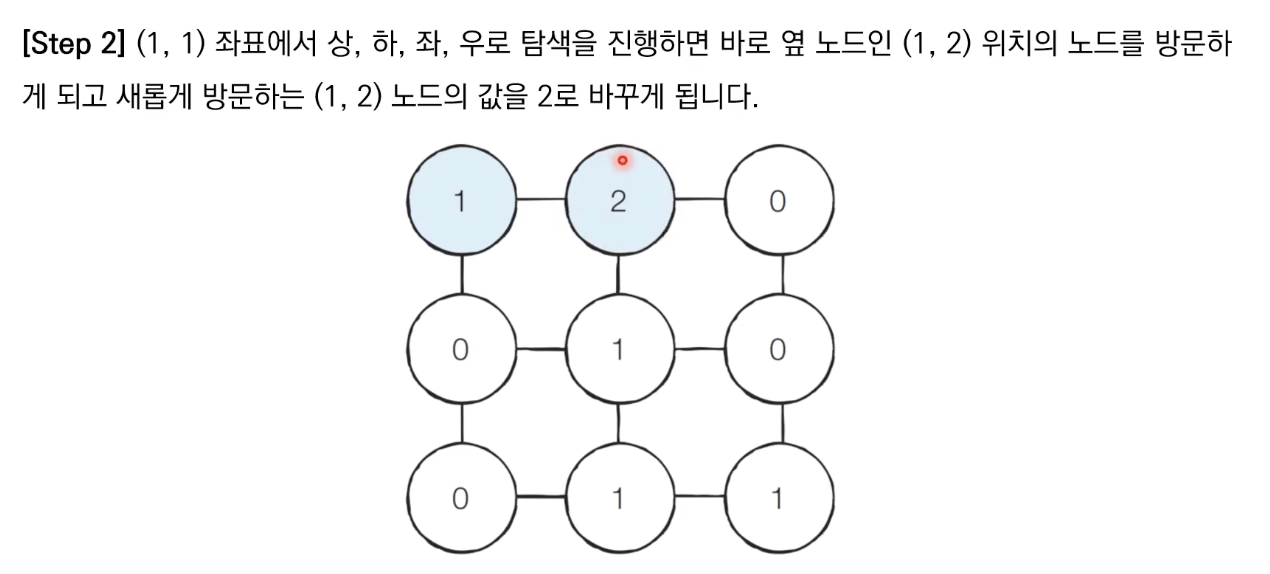

1. 입력 받기
먼저, 주어진 입력을 받아 코드로 표현합니다.
from collections import deque
# N, M을 공백을 기준으로 구분하여 입력 받기
n, m = map(int, input().split())
# 2차원 리스트의 맵 정보 입력 받기
graph = []
for i in range(n):
graph.append(list(map(int, input())))
2. 이동할 4가지 방향 정의 (상, 하, 좌, 우)
다음으로 이동할 수 있는 4가지 방향을 정의합니다.
앞서 말씀드린대로
상 -> (-1, 0)
하 -> (1, 0)
좌 -> (0, -1)
우 -> (0, 1)
이기 때문에, 이를 바탕으로 dx, dy를 정의할 수 있습니다.
# 이동할 네 가지 방향 정의 (상, 하, 좌, 우)
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
3. BFS 함수 정의
이후, bfs 함수를 정의하는데요,
# BFS 소스코드 구현
def bfs(x, y):
# 큐(Queue) 구현을 위해 deque 라이브러리 사용
queue = deque()
queue.append((x, y))
# 큐가 빌 때까지 반복하기
while queue:
x, y = queue.popleft()
# 현재 위치에서 4가지 방향으로의 위치 확인
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
# 미로 찾기 공간을 벗어난 경우 무시
if nx < 0 or nx >= n or ny < 0 or ny >= m:
continue
# 벽인 경우 무시
if graph[nx][ny] == 0:
continue
# 해당 노드를 처음 방문하는 경우에만 최단 거리 기록
if graph[nx][ny] == 1:
graph[nx][ny] = graph[x][y] + 1
queue.append((nx, ny))
# 가장 오른쪽 아래까지의 최단 거리 반환
return graph[n - 1][m - 1]
deque를 이용해 큐를 구현하고, 시작점을 큐에 추가합니다.
큐가 빌 때까지 반복하면서 현재 위치에서 for문을 통해 상, 하, 좌, 우로 이동 가능한 모든 위치를 확인합니다.
이 떄, 공간을 벗어난 경우나 벽인 경우를 무시하며,
해당 노드를 처음 방문하는 경우(1인 경우)에 현재 위치의 거리 + 1을 더하여 기록합니다.
전체 코드 및 동작 과정
from collections import deque
# N, M을 공백을 기준으로 구분하여 입력 받기
n, m = map(int, input().split())
# 2차원 리스트의 맵 정보 입력 받기
graph = []
for i in range(n):
graph.append(list(map(int, input())))
# 이동할 네 가지 방향 정의 (상, 하, 좌, 우)
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
# BFS 소스코드 구현
def bfs(x, y):
# 큐(Queue) 구현을 위해 deque 라이브러리 사용
queue = deque()
queue.append((x, y))
# 큐가 빌 때까지 반복하기
while queue:
x, y = queue.popleft()
# 현재 위치에서 4가지 방향으로의 위치 확인
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
# 미로 찾기 공간을 벗어난 경우 무시
if nx < 0 or nx >= n or ny < 0 or ny >= m:
continue
# 벽인 경우 무시
if graph[nx][ny] == 0:
continue
# 해당 노드를 처음 방문하는 경우에만 최단 거리 기록
if graph[nx][ny] == 1:
graph[nx][ny] = graph[x][y] + 1
queue.append((nx, ny))
# 가장 오른쪽 아래까지의 최단 거리 반환
return graph[n - 1][m - 1]
# BFS를 수행한 결과 출력
print(bfs(0, 0))
이제, 아래와 같은 예시 입력이 있을 때 동작 과정을 살펴봅시다!
5 6
101010
111111
000001
111111
111111
코드에 따라 graph는 아래와 같은 2차원 리스트로 초기화됩니다.
[
[1, 0, 1, 0, 1, 0],
[1, 1, 1, 1, 1, 1],
[0, 0, 0, 0, 0, 1],
[1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1]
]
초기 위치 (0, 0)에서 시작했다고 생각해봅시다.
이 때,
초기의 queue에는 [(0, 0)]이 담기게 됩니다.
-> 큐에 담긴 (0, 0)을 꺼내고 상하좌우로 이동이 가능한지 판단을 진행합니다.
상 : (-1, 0) -> 범위 벗어남
하 : (1, 0) -> 이동 가능 -> 거리 2로 갱신
좌 : (0, -1) -> 범위 벗어남
우 : (0, 1) -> 이동 불가 (0인 노드)
가 되며,
queue에는 [(1, 0)] 가 담기게 됩니다.
-> 역시 큐에 담긴 (1, 0)을 꺼내고 상하좌우로 이동이 가능한지 판단을 진행합니다.
이제 (0, 0) 에서 (1, 0)으로 이동을 하게 되죠.
(1, 0)을 기준으로
상 : (0, 0) -> 이미 방문
하 : (2, 0) -> 이동 불가 (0인 노드)
좌 : (1, -1) -> 범위 벗어남
우 : (1, 1) -> 이동 가능 (거리 3으로 갱신)
가 되며,
queue에는 [(1, 1)] 가 담기게 됩니다.
이와 같은 과정을 모두 반복하면 원하는 값을 얻을 수 있게 되죠.
느낀점
생각보다 DFS와 BFS의 차이가 잘 안 들어오는 것 같습니다.
많이 헷갈리기 때문에 열심히 문제를 풀어보고 익혀볼 수 있도록 노력해야겠습니다ㅠㅠ